感染、伝染に関しての数理モデルとしては、KermackとMcKendrick が1927年に提案した最も簡単な数理モデル(SIRモデル)[1] を採用することとします。
このモデルでは下記の微分方程式で表現されます。
\[\frac{dS}{dt} =- \beta SI\]
\[\frac{dI}{dt} = \beta SI- \gamma I\]
\[\frac{dR}{dt} = \gamma I\]
ここで、変数は$S$、$I$, $R$です。
$S$ は、the number of $susceptible$ individuals の $S$ であり, 感染の可能性のある個体の数量、すなわちまだ感染していない人の数(健康人口と呼ぶことにします)を表しています。
次に $I$ ,は, the number of $infected$ individuals の $I$ であり, 感染した個体の数量、すなわちすでに感染している人の数(感染人口と呼ぶことにします)を表しています。
変数 $R$ は、the number of $recovered$ individuals の $R$ であり、回復した個体の人数(回復人口と呼ぶことにします)を表しています。
なお $R$ には死者を含めます。
いっぽう、$\beta, \gamma>0 $ はパラメータです。
$\beta$ は、感染のしやすさを表すパラメータで感染率と呼ばれます。
$\gamma$ は、回復のしやすさを表すパラメータで回復率と呼ばれます。
上記微分方程式の第1式は、健康人口は健康人口 $S$ と感染人口 $I$の積 $SI$ に比例して減少することを表現しています。
第2式は、感染人口は健康人口 $S$ と感染人口 $I$ の積 $SI$ に比例して増加するとともに感染人口 $I$ に比例して減少することを表現しています。
第3式は、回復人口は感染人口 $I$ に比例して増加することを表現しています。
第1式と2式に非線形項 $SI$ がありますので、この数理モデルは非線形微分方程式となっていますことに注意してください。
非線形であるためこの微分方程式は解析解を求めることはできませんので、数値解析を行う必要があります。
次に、数値解析の一例を記載します。
数値解析には、scilabを利用しました。
初期値としては、 $S(0)=1000$, $I(0)=1$, $R(0)=0$ としました。
またパラメータ値としては、$\beta=0.0001$, $\gamma=0.07$ としてみました。
Figure 1 をご覧ください。
ここで、重要なことは以下です。
(1) 感染人口の時間変化は極大値をもち、その形状がピークじょうになること
(2) 健康人口の時間変化は、単調減少であること
(3) 回復人口の時間変化は、単調増加であること
(4) 感染人口、健康人口、回復人口の和は一定であること
事項(4)に関しては、上記微分方程式から導かれます。
すなわち、
\[\frac{dS}{dt} +\frac{dI}{dt}+\frac{dR}{dt} =- \beta SI0+\beta SI- \gamma I+\gamma I=0\]
から明らかです。
次回の考察では、新型コロナウィルスcovid-19に関してこの数理モデルを適用してみることにします。
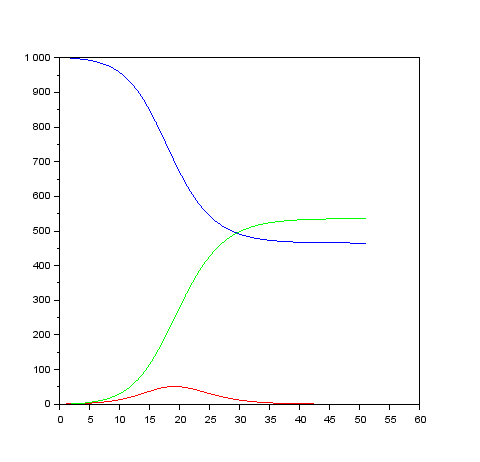
Figure 1 SIRモデルでの数値計算の一例
横軸は日数(日)、縦軸は人口(人)です。
青色カーブ:健康人口 $S(t)$ , 赤色カーブ:感染人口 $I(t)$, 緑色カーブ:回復人口 $R(t)$
$S(0)=1000$, $I(0)=1$, $R(0)=0$
$\beta=0.0001$, $\gamma=0.07$
[1]:https://www.maa.org/press/periodicals/loci/joma/the-sir-model-for-spread-of-disease-introduction







